微科盟扩增子和代谢组关联分析结题报告
一、概述
扩增子分析内容包括分类注释,物种筛选,基础统计,显著性差异比较,α多样性分析,β多样性分析等,旨在研究微生物群落菌群组成; 代谢组分析内容包括特征提取、标识代谢物、通路注释等,旨在获取代谢组的关键特征,例如代谢物种类、相对丰度、预测功能通路信息。
扩增子和代谢组关联分析是一种综合性的研究方法,运用多种统计学方法(如相关性分析,正交偏最小二乘分析等)来揭示微生物群落和代谢组之间的关联性,进而确定哪些微生物或功能与代谢物之间显著相关。流程旨在深入理解生物体内微生物群落(扩增子)和代谢产物(代谢组)之间的相互关系,以揭示它们在生物体健康和疾病中的功能和相互作用。
二、项目流程
关联分析流程基于R语言多个R包[1-8]。流程图1,关联分析的具体步骤如下:
1.代谢组数据标准化(样本内校正,含量矩阵校正,feature内校正),扩增子数据标准化(hellinger标准化)。
2.将关联分析分为两类:代谢物-物种关联分析,代谢物-功能关联分析。
3.相关性分析。
4.非监督类模型关联分析:PCA分析, Procrustes分析, PLS分析, RDA/CCA分析。
5.监督类模型关联分析:随机森林,支持向量机,模型的ROC评估曲线。
6.功能关联分析可以进行将两个组学数据共同进行富集分析并绘制通路图。
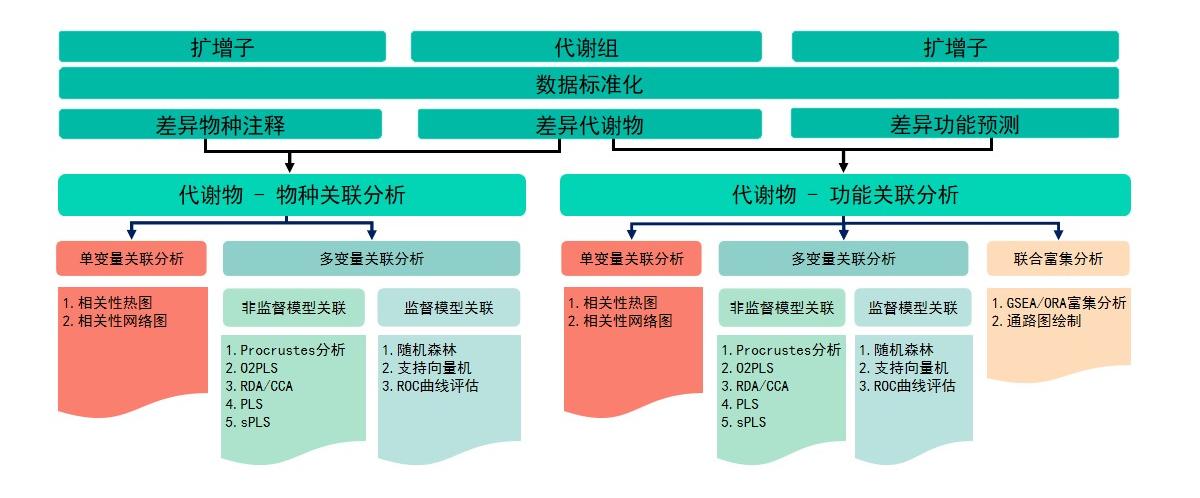
图1 关联分析流程
三、数据预处理
3.1 标准化校正
01.Normalization/ ├── metabolomic [代谢组数据] | ├──cpd_input_after_normalization.tsv [经过标准化的代谢组丰度表] | └──cpd_input_after_sample_normalization.tsv [只经过样本内校正的代谢组丰度表] └── Amplicon [扩增子数据] ├── All.KO.abundance_unstratified.hellinger_norm.tsv [hellinger标准化后的KO丰度表] └── All.Taxa.OTU.hellinger_norm.tsv [hellinger标准化后的物种注释丰度表]
在生科云的关联分析中,我们将代谢组数据进行了标准化校正,校正的步骤分为三步:
1.样本内校正:即样本里所有features的丰度除以该样本的丰度中位数(类似相对丰度计算);这是为了校正library size,在测定过程中,各个样本得到的总代谢物含量差异巨大, 而这种差异通常是样本采集和测定过程带来的系统误差,除以中位数,平均值,或者总和,都是校正这种系统误差的常用方式;
2.含量矩阵校正:即对所有含量值进行log转化;T检验以及ANOVA这样的差异比较方法,都要求代谢物含量服从正态分布,因此,我们一般用log转化,使得代谢物含量分布接近正态分布;
3.feature内校正:即feature对应的所有样本丰度减去该feature丰度均值再除以该feature丰度标准差;feature内校正的目的是使得所有代谢物的均值和标准差(或者说中位数,四分位点,scale)在同一个水平上; PCA,PLSDA,OPLSDA以及机器学习这样的分析,如果不进行代谢物的标准化,那么均值和标准差高的代谢物的重要性将会倾向于高于均值和标准差低的代谢物的重要性,而这样的结果显然不是我们想要的结果,在分组间差异大的才应该是重要性高的。
除了代谢组数据的标准化步骤,我们使用Hellinger转换方式对扩增子数据也进行了标准化预处理。标准化处理可以使不同组学数据的尺度一致。代谢组数据和扩增子数据可能具有不同的测量单位和数据范围,通过标准化,可以将它们调整到相同的尺度,使得它们可比性更强。Hellinger转换是物种注释和功能注释数据常用的转换方式,特别适用于处理丰度数据。这种转换方式通过将丰度数据的平方根与极端值缩小,降低了高丰度微生物的权重,减轻了不同维度之间的差异对分析结果的影响。
四、关联分析内容
4.1单变量关联分析
02.Univariate_Correlation_Analysis/ ├──Function.VS.Metabolites [功能注释-代谢物关联分析] | ├──KEGG | | ├──heatmap [相关性热图] | | └──network [相关性网络图] | ├──Other function library | └──... └──Species.VS.Metabolites [物种注释-代谢物关联分析] ├──heatmap [相关性热图] └──network [相关性网络图]
在代谢组和扩增子的关联分析中,网络图和相关性热图的绘制为研究提供了直观而全面的视觉展示,有助于深入理解两者之间的复杂关系。
4.1.1相关性热图
相关性热图先筛选丰度较高的features,然后应用Spearman相关性分析法进行分析,展示了代谢物和微生物的相关性系数,颜色的深浅表示相关性的强弱;P值小于0.001则标记为***,0.001<P<0.01则标记为**,0.01<P<0.05则标记为*。通过观察整个相关性热图,可以了解代谢物和微生物整体上的关联趋势。深色区域表示强烈的相关性,而浅色区域表示较弱的相关性;进而可以识别出代谢物与微生物之间的模式,例如聚类结构、明显的正相关或负相关群体。这有助于理解它们之间的协同变化和可能的生物学意义。 图中红色表示正相关,蓝色表示负相关;纵轴为扩增子features(如果是物种注释,则包含物种分类信息)或者功能注释,横轴为代谢物;默认展示宏基因组最相关的前20个features与代谢组最相关的前25个features。
图2-1 物种注释-代谢物 相关性热图
图2-2 功能注释-代谢物 相关性热图
4.1.2相关性网络图
网络图展示了代谢物和微生物群落之间的关联关系,每个节点代表一个代谢物或微生物,而连线表示它们之间的关联;网络图能够发现代谢物和微生物之间的正负相关关系,有助于生物学上的解释。通过节点的颜色、形状和大小等信息,可以推测出代谢物与微生物之间可能的共生关系、代谢途径的调控和互补作用。云流程一键化中默认设置的相关性系数阈值为0.2,相关性系数P-value阈值为0.05

图3-1 物种注释-代谢物 相关性网络图

图3-2 功能注释-代谢物 相关性网络图
4.2多变量关联分析
4.2.1非监督类模型分析
4.2.1.1Procrustes分析
03.Multivariate_Correlation_Analysis/ ├──Function.VS.Metabolites [功能注释-代谢物关联分析] | ├──KEGG | | ├──01.Procrustes [普鲁克分析] | | | ├──PCA_analysisReport_Omic1.txt [代谢组PCA分析报告] | | | ├──PCA_analysisReport_Omic2.txt [扩增子PCA分析报告] | | | ├──PCA_Biplot2.png [两个组学的PCA双标图] | | | ├──Procrustes_analysis_sites.tsv [普鲁克分析的坐标信息] | | | ├──Procrustes_residuals.tsv [普鲁克分析的残差值信息] | | | ├──procrustes_resultPlot.png [普鲁克分析图] | | | ├──Procrustes_resultReport.txt [普鲁克分析结果报告] | | | ├──protest_resultReport.txt [验证结果报告] | | | └──residuals_plot.png [残差值图] | | ├──02.PLS [PLS分析] | | ├──03.RDA_CCA [RDA/CCA分析] | | ├──04.RandomForest [随机森林分析] | | └──05.SVM [支持向量机分析] | ├──Other function library | └──... └──Species.VS.Metabolites [物种注释-代谢物关联分析] └──...
Procrustes分析是一种用于比较两个或多个数据集之间的相似性的方法[3], 由于扩增子与代谢组中,存在大量低丰度features,而这些features对于相关性分析贡献度极低,所以进行该模块分析之前,均根据丰度进行了features筛选,Procrustes分析适用于组学关联分析。这种分析通常涉及到PCA双标图、普氏分析图和残差值图等步骤:
PCA双标图:如图4-1通过主成分分析(PCA),将多维数据降维到较低维度, 然后在双标图上展示样本和变量在这些主成分上的分布,以便观察样本之间和变量之间的关系。 其中样本和变量在主成分上的投影用箭头和点表示。样本之间的距离和角度反映它们在主成分方向上的相似性或差异性。 不同箭头的方向之间的角度可以反映原始特征之间的相关性。如果两个箭头的方向相近,表示对应的特征在数据中可能存在相关性。 箭头的长度表示数据在主成分方向上的方差大小。较长的箭头表示在相关主成分上有更大的变化。因此, 箭头的长度可以用来衡量特征的重要性,对应的特征在数据变异性中的贡献更大。
图4-1 物种注释-代谢物 PCA双序图
图4-2 功能注释-代谢物 PCA双序图
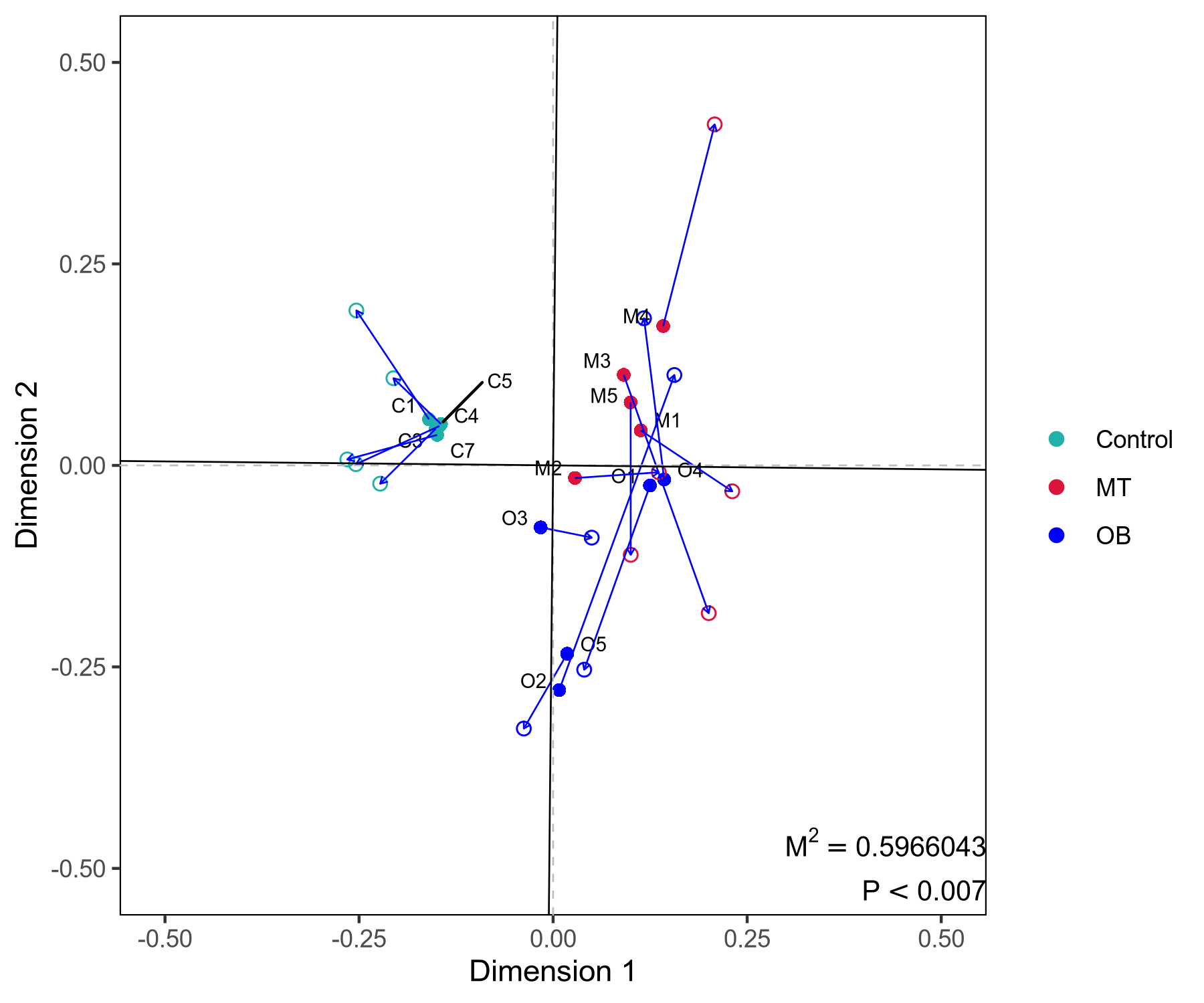
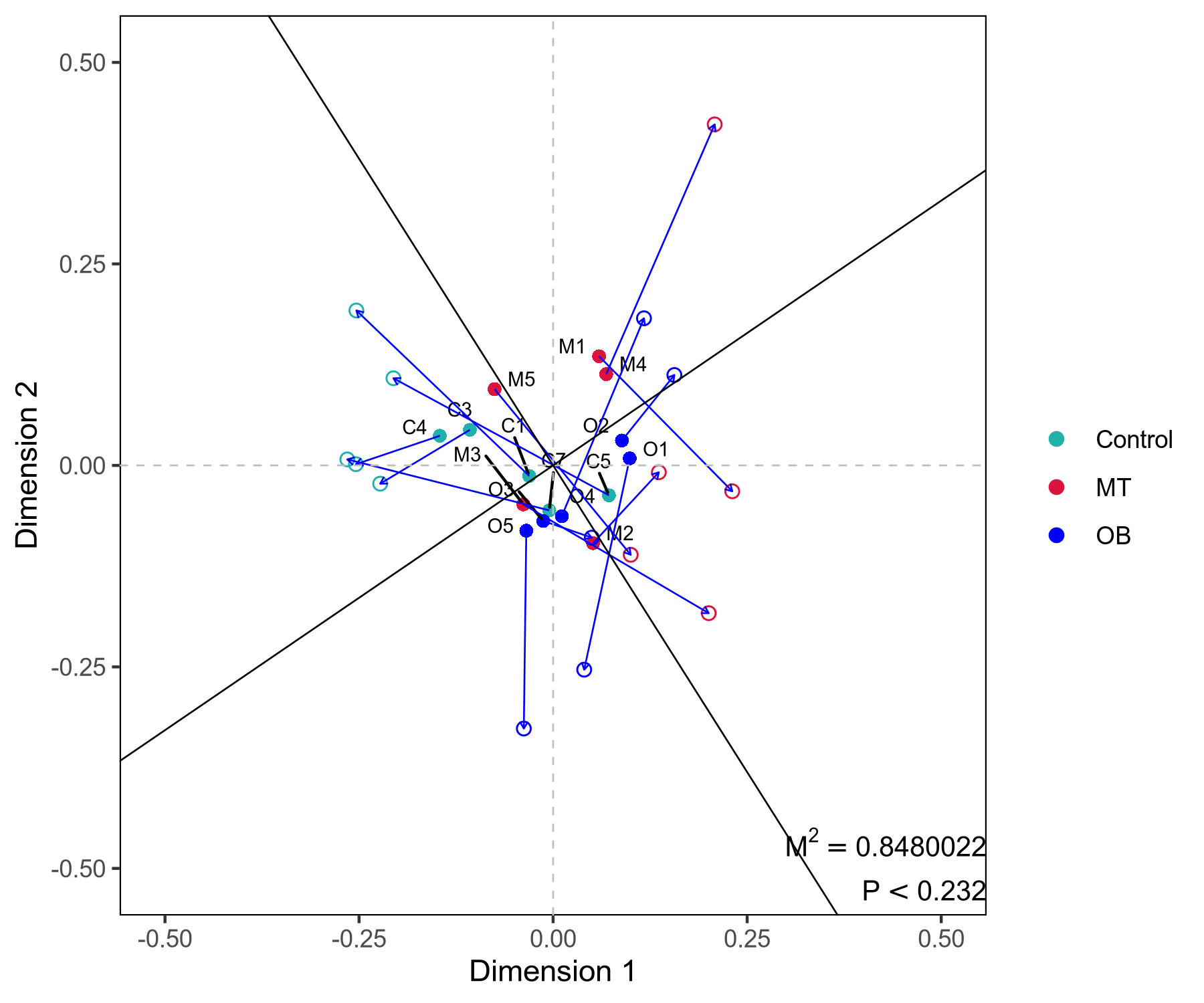
普鲁克分析图:通过普鲁克分析(Procrustes Analysis)对两个数据集进行旋转变换, 使它们在最佳方式下重叠,进一步揭示它们的相似性。结果中得到的旋转矩阵, 将一个数据集映射到另一个数据集的坐标系中。旋转图展示了这种映射关系, 帮助观察样本或变量之间的相似性。每个线段代表一个样本,线段一端实心圆点代表微生物组数据样本点, 线段另一端实心三角形代表相同样本的代谢组数据样本点;连线代表两排序构型的矢量残差, 可评价二者间的变异情况,连线越短,表示两个数据集之间一致性越高。M平方代表偏差平方和,是数据离散程度的指标。
(a)
(b)
图5 普鲁克分析图
注:(a),物种注释-代谢物 普鲁克分析;(b),功能注释-代谢物 普鲁克分析
残差值图:进行完普鲁克分析之后,通过比较两个数据集在主成分方向上的残差,揭示它们之间的差异。 残差是指样本点到主成分方向上的投影点之间的距离,残差值图展示了这些残差, 可以帮助识别哪些样本在两个数据集之间差异较大。如果样本中两个组学的组成更为相似, 则旋转图中两个匹配的点距离越近,残差较小,反之两个组学无规律,则残差更大。
图6-1 物种注释-代谢物 残差值图
图6-2 功能注释-代谢物 残差值图
4.2.1.2 PLS分析
03.Multivariate_Correlation_Analysis/ ├──Function.VS.Metabolites [功能注释-代谢物关联分析] | ├──KEGG | | ├──01.Procrustes [普鲁克分析] | | ├──02.PLS [PLS分析] | | | ├──ModelBuilding_parameters.csv [PLS建模参数预测结果] | | | ├──PLS_Features_correction_BarPlot.png [载荷值排序图] | | | ├──PLS_joint_loadings.png [联合载荷图] | | | ├──PLS_joint_scores.png [联合得分图] | | | ├──PLS_loadings.csv [联合载荷值信息表] | | | └──PLS_scores.csv [联合得分值信息表] | | ├──03.RDA_CCA [RDA/CCA分析] | | ├──04.RandomForest [随机森林分析] | | └──05.SVM [支持向量机分析] | ├──Other function library | └──... └──Species.VS.Metabolites [物种注释-代谢物关联分析] └──...
偏最小二乘法(partial least squares,PLS)PLS分析是一种多变量分析方法,主要用于探索两组变量之间的关系,以揭示变量之间复杂的相互作用和关联。PLS通过寻找最能解释X和Y之间共变异的成分来简化模型,有助于在小样本情况下提高模型的稳定性和预测能力。 PLS分析通过对两个数据组间的整合分析,评估两个数据集之间的内在相关性[4]。PLS模型一方面可反映不同数据组间的整体影响, 另一方面可直接体现不同变量在模型中的权重,权重越大,意味着该变量的变化对另一个组学的扰动更剧烈。该分析模块分为三个部分: 联合载荷图,联合得分图,关联程度最大的features柱状图。
联合载荷图(Joint loadings plot):该图显示了两个数据矩阵之间的共同结构,即它们之间的关联性。 如果该图是二维散点图,则X轴和Y轴分别代表了PLS第一成分loadings值和PLS第二成分loadings值,每个点表示一个features,点的位置和方向表示该features在两个数据集中的权重和方向。联合载荷图的X轴和Y轴值的大小和方向反映了变量在两个组学数据集之间的关系; 正值和负值表示features在两个数据集中的相关性方向,值的大小表示features对另一个组学的关联程度。features在图中的位置和包裹趋势则表明它们在两个数据集中的共同结构上的重要性和方向。 这些观察可以帮助解释两个组学数据集之间的关联性和共同模式。
(a)
(b)
图7 联合载荷图
注:(a),物种注释-代谢物 联合载荷图;(b),功能注释-代谢物 联合载荷图
联合得分图(Joint score plot):Joint scores图展示了每个样本在PLS中的投影,即它们在共同结构上的表现。 这反映了样本在两个数据集之间的关联性。正负值反映了样本在两个组学数据集之间的相关性方向; 样本在图中的相对位置反映了它们在两个组学数据集之间的关联性, 相邻或聚集的样本可能在两个数据集中表现相似。
(a)
(b)
图8 联合得分图
注:(a),物种注释-代谢物 联合得分图;(b),功能注释-代谢物 联合得分图
最后选择前两个维度(joint loadings1、joint loadings2)载荷值长度前15的features(关联程度最大)绘制柱状图。
(a)
(b)
图9 载荷值排序图
注:(a),物种注释-代谢物 载荷值排序图;(b),功能注释-代谢物 载荷值排序图
4.2.1.3RDA/CCA分析
03.Multivariate_Correlation_Analysis/ ├──Function.VS.Metabolites [功能注释-代谢物关联分析] | ├──KEGG | | ├──01.Procrustes [普鲁克分析] | | ├──02.PLS [PLS分析] | | ├──03.RDA_CCA [RDA/CCA分析] | | | ├──DCA_output.xls [DCA分析结果表格] | | | ├──groups_RDA.envfit.xls [代谢组对扩增子影响值表格] | | | ├──groups_RDA.Factors.PERMANOVA.xls [PERMANOVA分析报告_features因子] | | | ├──groups_RDA.features.xls [features影响值表格] | | | ├──groups_RDA.Group.PERMANOVA.xls [PERMANOVA分析报告_样本分组] | | | ├──groups_RDA.sample.xls [样本影响值表格] | | | ├──groups_RDA_features_location_plot.png [features RDA双序图] | | | ├──groups_RDA_sample_location_plot.png [样本 RDA双序图] | | | └──groups_RDA_sample_location_plot_with_labels.png [样本 RDA双序图(带标签)] | | ├──04.RandomForest [随机森林分析] | | └──05.SVM [支持向量机分析] | ├──Other function library | └──... └──Species.VS.Metabolites [物种注释-代谢物关联分析] └──...
RDA和CCA都属于冗余分析(Redundancy Analysis)的范畴, 都是在解释一个变量组对另一个变量组的方差贡献时进行的, 云流程会根据数据特点自动挑选RDA或者CCA分析。 旨在用统计学手段建立两个组学features之间的回归关系,保留能解释的变异, 后将features进行降维,通过夹角指示相关性。箭头的长度表示代谢物在RDA轴上的投影的强度, 较长的箭头表示该代谢物在相应RDA轴方向上的贡献较大,与扩增子的变化有关, 长箭头指示了代谢物与扩增子数据的关联性更强,对相应的轴有更大的贡献; 箭头与扩增子features点的夹角表示代谢物与扩增子的关联性,以及这个关联性的方向。 小夹角表示代谢物和相应的扩增子特征在RDA轴上有相似的变化趋势, 表明它们之间可能存在关联性。 样本RDA双序图中的p值反映了分组对微生物差异的解释程度,p小于0.05,则解释方差显著。
(a)
(b)
图10 features RDA双序图
注:(a),物种注释-代谢物 features RDA双序图;(b),功能注释-代谢物 features RDA双序图
(a)
(b)
图11 样本RDA双序图
注:(a),物种注释-代谢物 样本RDA双序图;(b),功能注释-代谢物 样本RDA双序图
4.2.2监督类模型分析
4.2.2.1随机森林
03.Multivariate_Correlation_Analysis/ ├──Function.VS.Metabolites [功能注释-代谢物关联分析] | ├──KEGG | | ├──01.Procrustes [普鲁克分析] | | ├──02.PLS [PLS分析] | | ├──03.RDA_CCA [RDA/CCA分析] | | ├──04.RandomForest [随机森林分析] | | | ├──Metabolomic_model_Error_Rate_Curve.png [代谢组RandomForest模型错误率曲线图] | | | ├──Metabolomic_model_Probability_Graph_Of_Correctly_Classified.png [代谢组RandomForest模型样本裕度图] | | | ├──Metabolomic_RFimportance.tsv [代谢组RandomForest模型中features重要性信息] | | | ├──MetabolomicROC_curve_specificities_ofRandomForest.tsv [代谢组RandomForest模型ROC曲线信息] | | | ├──Amplicon_model_Error_Rate_Curve.png [扩增子RandomForest模型错误率曲线图] | | | ├──Amplicon_model_Probability_Graph_Of_Correctly_Classified.png [扩增子RandomForest模型样本裕度图] | | | ├──Amplicon_RFimportance.tsv [扩增子RandomForest模型中features重要性信息]] | | | ├──AmpliconROC_curve_specificities_ofRandomForest.tsv [扩增子RandomForest模型ROC曲线信息] | | | ├──RFMeanDecreaseAccuracy.png [两个组学RandomForest模型features重要性图] | | | └──ROC_of_RFmodel.png [两个组学RandomForest模型ROC评估曲线图] | | └──05.SVM [支持向量机分析] | ├──Other function library | └──... └──Species.VS.Metabolites [物种注释-代谢物关联分析] └──...
随机森林是一种集成学习方法[1],它通过构建多个决策树,每个树都在不同的子样本和特征上训练, 最后将它们的结果综合起来。这种集成方法有效地减小了过拟合的风险,并且对于高维数据集表现良好。 随机森林能够输出每个特征的重要性评分,即特征对于模型性能的贡献程度。这些重要性分数可以用来筛选最相关的特征, 帮助识别与实验组和对照组差异相关的生物学特征。随机森林关联分析的目的是利用多个决策树的集成效果,获取两种组学间, 各features的重要性比较,并通过不同组学的单独建模的ROC曲线(受试者回归曲线, Receiver Operating Characteristic curve)对比,评估哪种组学能更好地分离对照组和实验组。 随机森林分析,云流程默认选择贡献值前25个features进行柱形图展示,其他features的贡献值请见表格。
注意:在多分类模型中(分组方案中存在多个分组),绘制ROC曲线通常是通过将每个类别与其他所有类别结合起来进行二分类来完成的。这是因为ROC曲线是针对二分类问题设计的,它显示了真正例率(True Positive Rate,也称为灵敏度)和假正例率(False Positive Rate)之间的关系。 在多分类情况下,可以将每个类别视为一个正例,其他所有类别合并为一个负例,然后分别计算每个类别的真正例率和假正例率,最终将这些结果绘制在同一张ROC曲线上。
图12-1 物种注释-代谢物 随机森林features重要性排序图
图12-2 功能注释-代谢物 随机森林features重要性排序图
图13-1 物种注释-代谢物 随机森林模型ROC图
图13-2 功能注释-代谢物 随机森林模型ROC图
4.2.2.2支持向量机
03.Multivariate_Correlation_Analysis/ ├──Function.VS.Metabolites [功能注释-代谢物关联分析] | ├──KEGG | | ├──01.Procrustes [普鲁克分析] | | ├──02.PLS [PLS分析] | | ├──03.RDA_CCA [RDA/CCA分析] | | ├──04.RandomForest [随机森林分析] | | └──05.SVM [支持向量机分析] | | | ├──Metabolomic_SVM_features_importance.tsv [代谢组SVM模型features重要性信息] | | | ├──MetabolomicROC_curve_specificities_ofSVM.tsv [代谢组SVM模型ROC曲线信息] | | | ├──Amplicon_SVM_features_importance.tsv [扩增子SVM模型features重要性信息] | | | ├──AmpliconROC_curve_specificities_ofSVM.tsv [扩增子SVM模型ROC曲线信息] | | | ├──ROC_of_SVMmodel.png [两个组学SVM模型ROC曲线图] | | | └──SVM_FeaturesImportance.png [两个组学SVM模型features重要性图] | ├──Other function library | └──... └──Species.VS.Metabolites [物种注释-代谢物关联分析] └──...
支持向量机是一种监督学习算法[5],其目标是找到一个超平面,将不同类别的样本分隔开。 在生物信息学中,SVM可以用于分类和回归任务。SVM在分类问题中对样本之间的复杂关系有较好的拟合能力。 支持向量机的支持向量也可以提供有关差异性特征的信息。 除了两个组学features比较以外,与随机森林一样,提供组学分别建模的ROC曲线比较。
扩增子和代谢组的数据通常是高维度的,其中包含了大量的features。随机森林在高维数据中表现优异, 因为它可以自动选择子集进行训练,从而减小过拟合风险。相比之下,支持向量机在高维数据中的性能高度依赖于核函数的选择和参数调整; 随机森林相对于异常值具有较好的鲁棒性,因为它基于多个决策树的综合结果,异常值对于整体的影响较小。支持向量机在某些情况下可能对异常值较为敏感, 因为它试图找到一个全局最优的超平面,受到极端值的影响较大。 支持向量机分析,云流程默认选择贡献值前25个features进行柱形图展示,其他features的贡献值请见表格。
注意:在多分类模型中(分组方案中存在多个分组),绘制ROC曲线通常是通过将每个类别与其他所有类别结合起来进行二分类来完成的。这是因为ROC曲线是针对二分类问题设计的,它显示了真正例率(True Positive Rate,也称为灵敏度)和假正例率(False Positive Rate)之间的关系。 在多分类情况下,可以将每个类别视为一个正例,其他所有类别合并为一个负例,然后分别计算每个类别的真正例率和假正例率,最终将这些结果绘制在同一张ROC曲线上。
图14-1 物种注释-代谢物 支持向量机features重要性排序图
图14-2 功能注释-代谢物 支持向量机features重要性排序图
图15-1 物种注释-代谢物 支持向量机模型ROC图
图15-2 功能注释-代谢物 支持向量机模型ROC图
4.3联合富集分析
4.3.1筛选差异features
04.Features_Select [挑选差异features] ├──Compound [代谢物] | ├──Ttest_Volcano_features_significance.tsv [T-test差异分析结果] | └──Ttest_volcano.png [T-test火山图] └──KO [KO基因集] ├──group_MET.vs.Control_All.xls [deseq2差异分析的完整结果] ├──group_MET.vs.Control_DEG.xls [deseq2差异分析的显著差异结果] └──group_MET.vs.Control_Volcano.png [deseq2火山图]
在关联分析中,扩增子是离散型计数数据,T-test对于离散计数数据的分析往往并不合适, 因为它对数据的正态性和方差齐性有一定要求,因此对于扩增子数据,我们推荐使用deseq2/edgeR[6,7]进行差异features筛选, deseq2/edgeR使用负二项分布模型来考虑数据的离散性和过度离散性,对差异分析提供了较为准确的估计。而代谢组数据, 因为属于浓度测定,作为连续型数据,结题报告中采用T-test方法进行差异分析,而DESeq2是为处理类似于RNA-Seq的离散计数数据而设计的, 在此之前,代谢组数据已先进行过标准化处理, 使数据满足正态分布的特征,更符合T-test分析的要求。

(a)
(b)
图16 筛选差异features
注:(a),代谢物T-test火山图;(b),KO功能注释deseq2火山图
4.3.2ORA富集分析
05.Enrichment_Analysis/ ├──01.ORA [ORA富集分析] | ├──kegg_enrichmentORA.tsv [ORA富集分析结果表格] | ├──Enrichment_bubblePlot_ORA.png [ORA富集分析气泡图] | └──enrichPath_map [显著富集的KEGG通路] | └──... └──02.GSEA [GSEA富集分析]
富集分析的目的寻找在某个生物学过程中起关键作用的生物通路,从而揭示和理解生物学过程的基本分子机制[8]。 将扩增子KO注释和代谢物数据整合成一个综合的背景基因集,其中包含了扩增子和代谢物的信息, 在关联分析中,我们进行了ORA联合富集分析,使用T-test、DeSeq2筛选过的KO基因和代谢物作为输入, 对整合的背景基因集进行关联富集分析(也可以使用其他筛选方式进行features筛选或者不筛选,该部分可在云流程步骤中进行单独调整)。这将揭示哪些KO和代谢物在某些通路中同时富集。除此以外,我们将显著富集的通路进行展示。
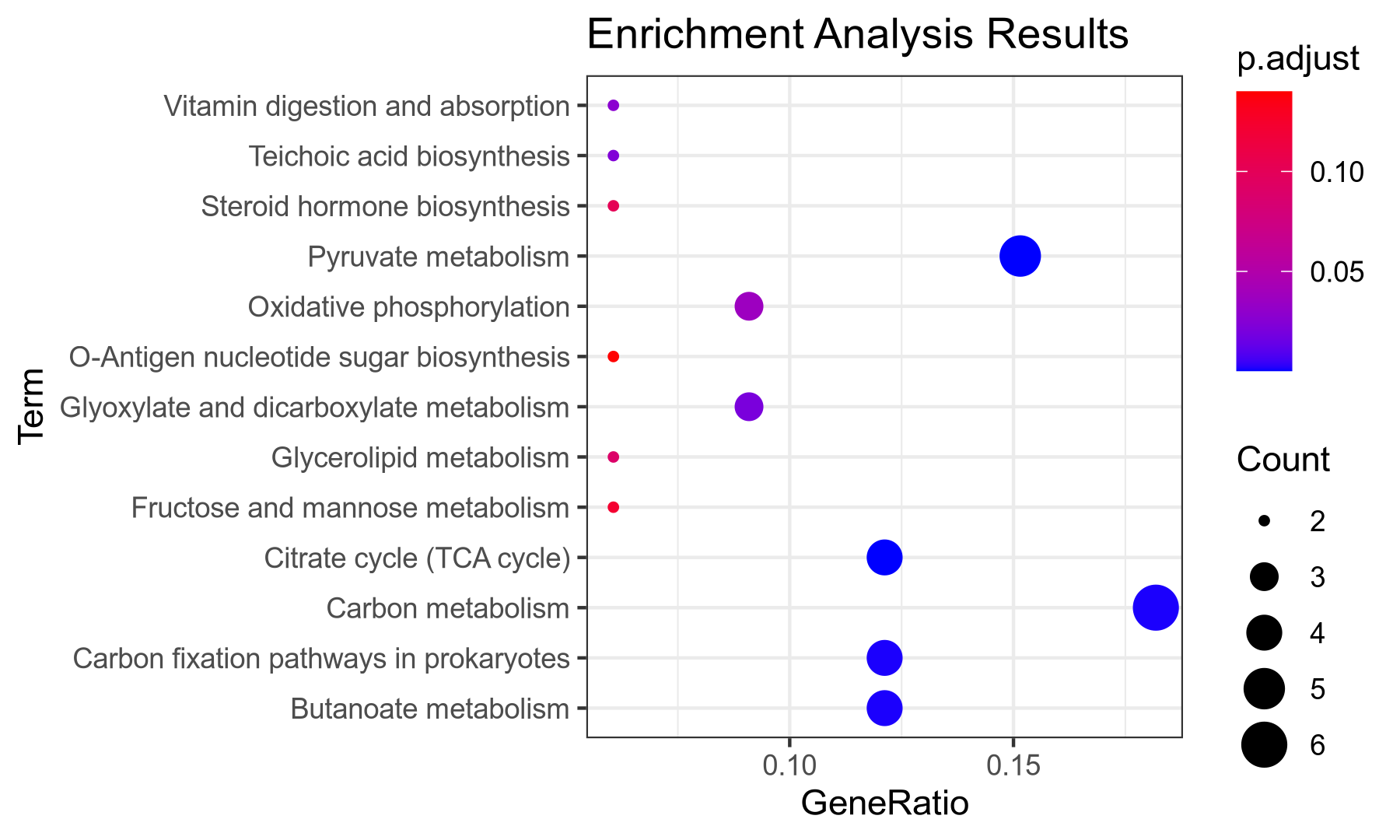
图17 ORA富集分析气泡图
图18 ORA显著富集通路
- 图中是同时包含代谢物和基因的KEGG代谢通路,有颜色的代谢物或KO基因是在分组间有显著差异的features
- 图中标注features的颜色反应其FC(fold change)水平;图片右上角有详细标尺,红色和绿色代表KO基因集的FC正负水平,黄色和蓝色代表代谢物的FC正负水平
4.3.3GSEA富集分析
05.Enrichment_Analysis/
├──01.ORA [ORA富集分析]
└──02.GSEA [GSEA富集分析]
├──kegg_enrichmentGSEA.tsv [GSEA富集分析结果表格]
├──Enrichment_bubblePlot_GSEA.png [GSEA富集分析气泡图]
├──Enrichment_GSEAcurvePlot.png [GSEA富集曲线图]
└──enrichPath_map [显著富集的KEGG通路]
└──...
云流程中,我们也添加了两个组学GSEA的关联富集分析。GSEA是一种全局性的富集分析方法, 不仅关注丰度存在差异的features,还考虑整体数据中基因的features丰度顺序。这有助于发现整体上的生物学趋势和通路变化。 GSEA在小样本数据集上的性能相对较好,能够处理样本量较少的实验设计。显著富集的通路,我们将全部进行展示。不同于ORA分析,GSEA分析使用Fold change值进行富集分析,分析筛选较为苛刻, 所以在结题报告中,我们选择了两个组学全部features进行了GSEA富集分析(也可以使用筛选方式,该部分可在云流程步骤中进行单独调整)。
给定一个预先定义的基因集S(如一个GO条目的成员基因集),和一个依据某个指标排好序的基因列表L(本报告中L采用所有基因的log2FoldChange排序), GSEA的目的在于检验S的成员是随机分散在L中(p.adjust>0.05),还是主要集中在L的底部或者顶部(p.adjust<0.05); 在富集结果中的p.adjust< 0.05也就意味着对应富集条目(如某个GO条目或者KEGG通路)的大部分成员基因低表达,或者高表达。
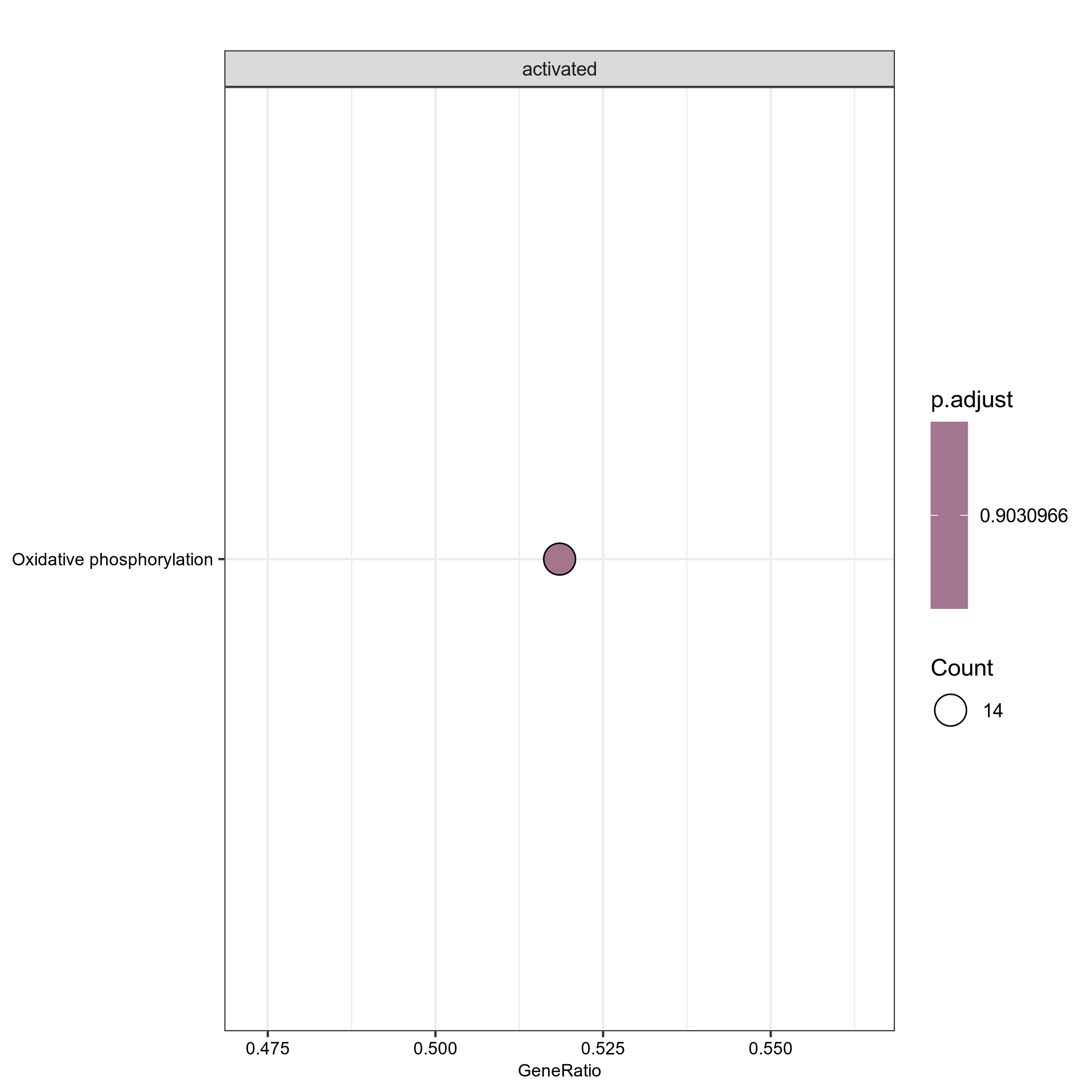
图19 GSEA富集分析气泡图
除富集结果图外,GSEA分析中富集分析曲线图用于反映基因集在整个排序数据集中的富集程度。 富集分析曲线图是用于反映基因集在整个排序数据集中的富集程度。X轴通常表示features集合的成员在整个排序基因集中的相对位置。 排序是通过丰度数据进行排序的,通常是按照features的差异性、表达量等排序的结果。Y 轴表示富集得分(Enrichment Score, ES)。 富集得分是一种度量基因集在排序基因集中的集中程度的指标。富集得分越高,表示基因集在排序基因集中的成员更趋向于聚集在一起。 正的富集得分表示基因集在排序基因集的上部富集, 而负的富集得分表示基因集在下部富集。富集得分的绝对值越大,表示富集效应越显著。
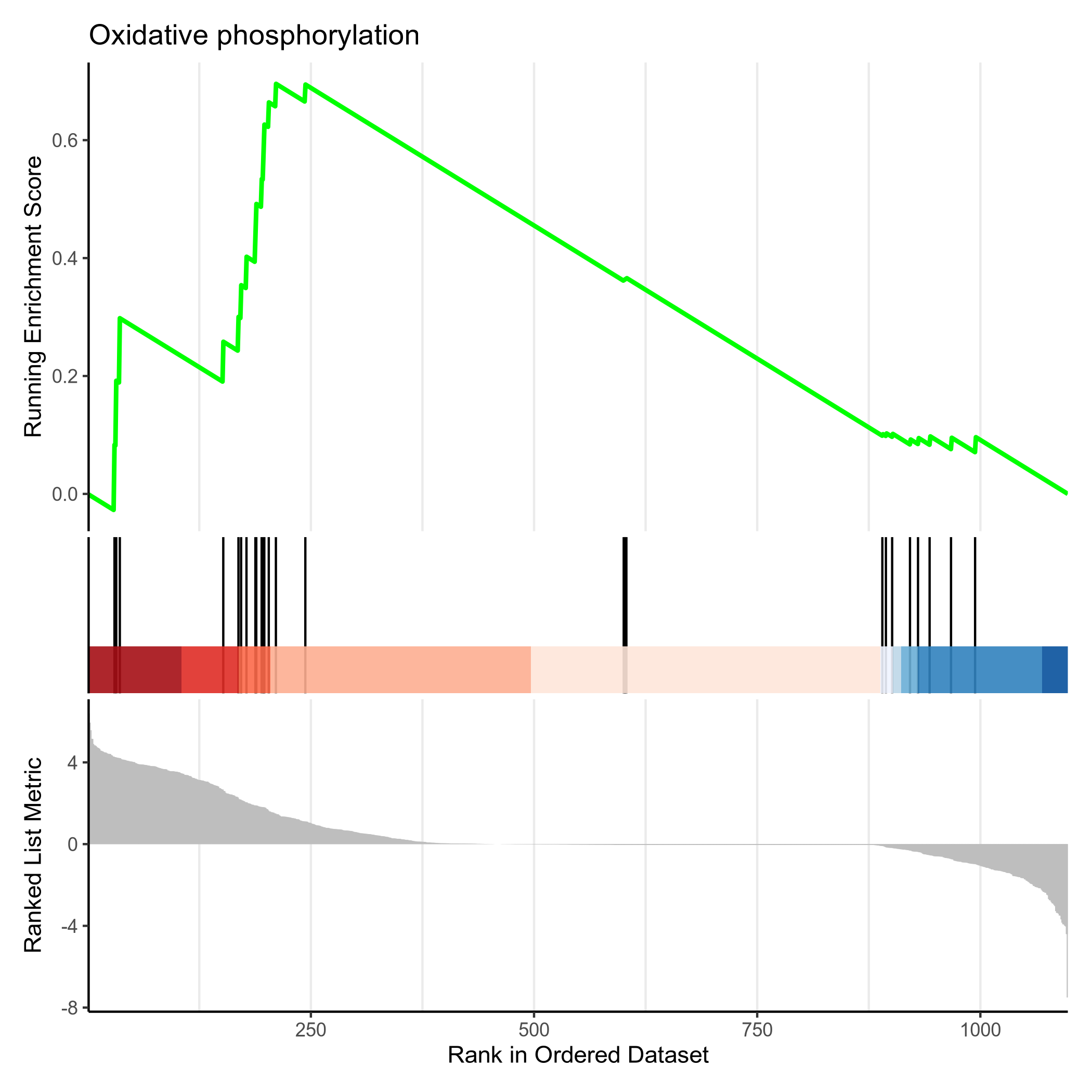
图20 GSEA富集分析曲线图
- 该图分为三部分。横坐标都代表排好序的基因列表L,如1代表log2FoldChange最高的基因。
- 对于上部分:纵坐标Running Enrichment Score的计算方式如下:从基因集L的第一个基因开始,计算一个累计统计值。当遇到一个落在S里面的基因,则增加统计值。 遇到一个不在S里面的基因,则降低统计值。如果S的成员是随机分散在L中,则对应基因集的线(某个KEGG通路的线,一种颜色代表一个KEGG通路)应该是平缓的。 如果存在一个单峰,则表示大部分S的成员聚集在峰的区域(不包含峰后面的部分),该区域的基因即富集结果中的core_enrichment列(S的子集), 该单峰的纵坐标即为富集得分(富集结果中的enrichmentScore),横坐标即为enrich.xls的rank列。
- 中间部分用竖线代表S的成员(某个KEGG通路的成员),有竖线,代表S包含该基因(KEGG通路包含该基因),竖线密集的地方就是Running Enrichment Score峰值出现的部位,每种颜色代表一个单独的S(KEGG通路)
- 下部分展示了排好序的基因列表L的排序指标,这里的纵坐标就是log2FoldChange。
图21 GSEA显著富集通路
- 图中是同时包含代谢物和基因的KEGG代谢通路,有颜色的代谢物或KO基因是在分组间有显著差异的features
- 图中标注features的颜色反应其FC(fold change)水平;图片右上角有详细标尺,红色和绿色代表KO基因集的FC正负水平,黄色和蓝色代表代谢物的FC正负水平
五、分析所用软件的版本
| 软件 | 版本 |
|---|---|
| ggplot2 | 4.2.3 |
| vegan | 4.2.3 |
| OmicsPLS | 4.2.3 |
| igraph | 4.2.3 |
| pheatmap | 4.2.3 |
| randomForest | 4.2.2 |
| e1071 | 4.2.3 |
| pROC | 4.2.3 |
| pathview | 4.2.1 |
| DESeq2 | 1.26.0 |
| edgeR | 3.28.1 |
| clusterProfiler | 3.14.3 |