微科盟扩增子和转录组关联分析结题报告

一、概述

扩增子分析内容包括物种组成分析、丰度分析、功能注释等，旨在获取扩增子的关键特征，例如微生物种类、丰度信息和潜在的功能通路；转录组分析内容包括可变剪切分析、蛋白互作分析、富集分析等，旨在获取物种的关键基因。

扩增子和转录组关联分析的目的是通过整合两种不同类型的生物数据来揭示微生物群落与宿主基因表达之间的关系。进而识别特定微生物与宿主基因表达之间的相关性，揭示微生物如何影响宿主的生理功能和疾病状态。

二、项目流程

关联分析流程基于R语言多个R包^[1-7]。流程图1，关联分析的具体步骤如下：

1.转录组数据标准化（TPM计算），扩增子数据标准化（hellinger标准化）。

2.将关联分析分为两类：宿主基因-扩增子物种关联分析，宿主基因-扩增子基因关联分析。

3.相关性分析。

4.回归分析。

5.非监督类模型关联分析：PCA分析, Procrustes分析, PLS分析, sPLS分析, O2PLS分析, RDA/CCA分析。

6.监督类模型关联分析：随机森林，支持向量机，模型的ROC评估曲线。

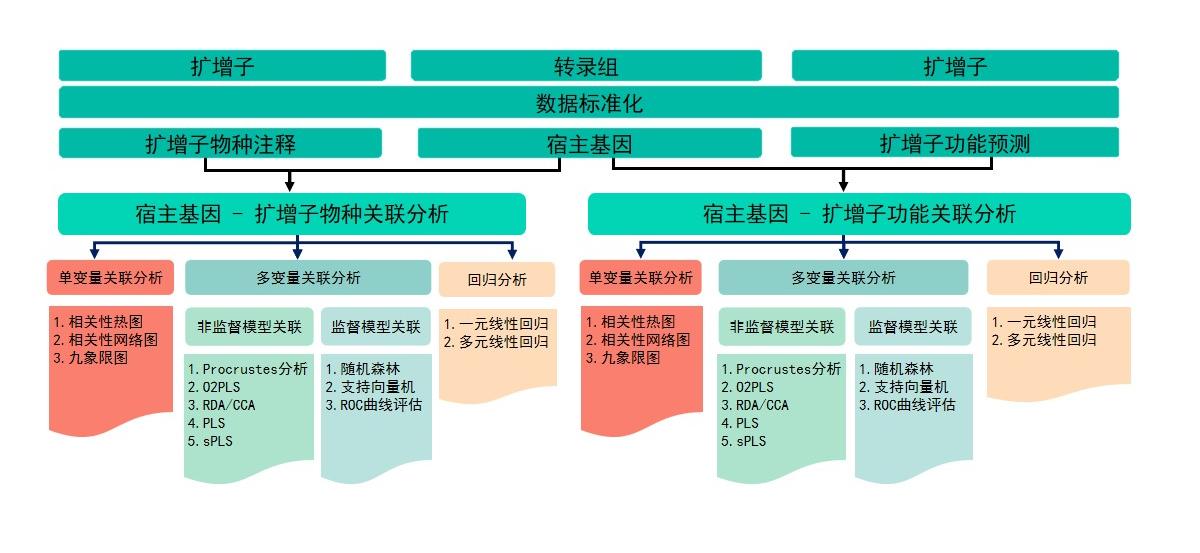
图1 关联分析流程

三、数据预处理

3.1 标准化校正

01.Normalization/
├── Transcriptome         [转录组数据]
|   └──input_Trans.tsv                                         [转录组预处理结果数据]
└── Amplicon              [扩增子数据]
    ├── All.KO.abundance_unstratified_hellinger_norm.tsv       [hellinger标准化后的KO丰度表]
    ├── All.KO.abundance_unstratified_sample_normalization.tsv [样本内标准化后的KO丰度表]
    ├── All.Taxa.OTU_hellinger_norm.tsv                        [hellinger标准化后的物种注释丰度表]
    ├── All.Taxa.OTU_sample_normalization.tsv                  [样本内标准化后的物种注释丰度表]
    └──...

标准化结果位置如下：analysis_files/01_Normalization

转录组数据进行TPM（Transcripts Per Million）标准化的原因主要是为了使得不同样本之间的基因表达水平具有可比性，以下是具体原因和原理：

消除测序深度的影响：不同样本的测序深度（即总的测序读取数）可能不同，直接比较原始的读取数会导致不准确的结果。TPM通过将基因的表达水平标准化为每百万读取数，可以消除这种差异。

消除基因长度的影响：基因长度的差异也会影响基因的表达水平。长基因比短基因更容易获得更多的读取数，因此需要对基因长度进行校正。TPM通过每千碱基读取数来调整基因长度的影响，使得不同长度基因的表达水平具有可比性。

跨样本比较：标准化后的TPM值可以用于不同样本之间的比较，因为它们已经消除了测序深度和基因长度的影响。这对于转录组研究中的差异表达分析和关联分析非常重要。

除了转录组数据的标准化步骤，我们使用Hellinger转换方式对扩增子丰度数据也进行了标准化预处理。标准化处理可以使不同组学数据的尺度一致。转录组数据和扩增子数据可能具有不同的测量单位和数据范围，通过标准化，可以将它们调整到相同的尺度，使得它们可比性更强。 Hellinger转换是物种注释与功能注释常用的转换方式，特别适用于处理丰度数据。这种转换方式通过将丰度数据的平方根与极端值缩小，降低了高丰度微生物的权重，减轻了不同维度之间的差异对分析结果的影响。

结题报告中，仅展示扩增子单一功能注释或物种注释的关联分析，其他功能数据库、物种数据库的关联分析可在一键化流程中，选取您期望的输入文件，或者在云流程中分步骤运行分析。

四、关联分析内容

4.1单变量关联分析

02.Univariate_Correlation_Analysis/
├──Function.VS.Transcriptome             [功能注释-宿主基因关联分析]
|  ├──heatmap  [相关性热图]
|  └──network  [相关性网络图]
└──Species.VS.Transcriptome              [物种注释-宿主基因关联分析]
   ├──heatmap  [相关性热图]
   └──network  [相关性网络图]

在转录组和扩增子的关联分析中，网络图和相关性热图的绘制为研究提供了直观而全面的视觉展示，有助于深入理解两者之间的复杂关系。

4.1.1相关性热图

相关性热图先筛选丰度较高的features，然后应用Spearman相关性分析法进行分析，展示了宿主基因和微生物的相关性系数，颜色的深浅表示相关性的强弱；P值小于0.001则标记为***，0.001<P<0.01则标记为**，0.01<P<0.05则标记为*。通过观察整个相关性热图，可以了解宿主基因和微生物整体上的关联趋势。深色区域表示强烈的相关性，而浅色区域表示较弱的相关性；进而可以识别出宿主基因与微生物之间的模式，例如聚类结构、明显的正相关或负相关群体。这有助于理解它们之间的协同变化和可能的生物学意义。图中红色表示正相关，蓝色表示负相关；纵轴为扩增子features(如果是物种注释，则包含物种分类信息)或者功能注释，横轴为转录组基因。使用的R包包括pheatmap，psych。

功能相关性热图分析结果位置如下：analysis_files/02_Univariate_Correlation_Analysis/Function.VS.Transcriptome/heatmap

物种相关性热图分析结果位置如下：analysis_files/02_Univariate_Correlation_Analysis/Taxa.VS.Transcriptome/heatmap

图2-1 物种注释-宿主基因相关性热图

图2-2 功能注释-宿主基因相关性热图

说明：纵轴为扩增子features(如果是物种注释，则包含物种分类信息)。横轴为宿主基因。图中上方的聚类树为宿主基因的相似度聚类，左侧的聚类树为扩增子features聚类树，中间的热图是两个组学之间的相关性热图，颜色与相关性值的关系见图右上方的刻度尺。

4.1.2相关性网络图

网络图展示了宿主基因和扩增子物种注释或者功能注释之间的关联关系，每个节点代表一个宿主基因或物种/功能注释，而连线表示它们之间的关联；网络图能够发现宿主基因和微生物之间的正负相关关系，有助于解释宿主与微生物的关系。使用的R包包括psych，igraph。

功能相关性网络图分析结果位置如下：analysis_files/02_Univariate_Correlation_Analysis/Function.VS.Transcriptome/network

物种相关性网络图分析结果位置如下：analysis_files/02_Univariate_Correlation_Analysis/Taxa.VS.Transcriptome/network

图3-1 物种注释-宿主基因相关性网络图

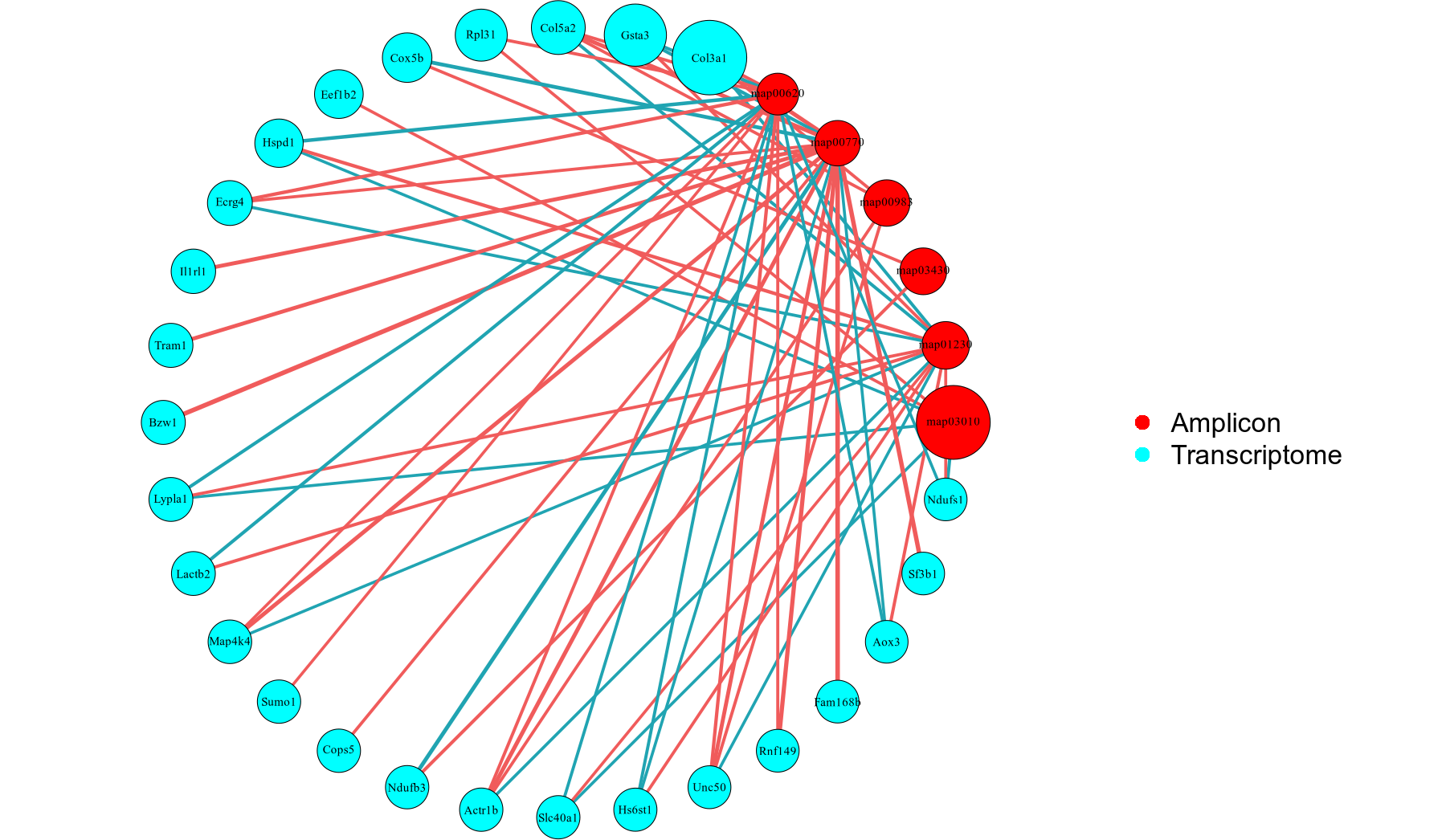
图3-2 功能注释-宿主基因相关性网络图

说明：该图中，红色圆形代表扩增子features，蓝色圆形代表宿主基因，圆圈的大小代表features丰度；各features间的连线，蓝色代表负相关，红色代表正相关。

4.2多变量关联分析

4.2.1非监督类模型分析

4.2.1.1Procrustes分析

03.Multivariate_Correlation_Analysis/
├──Function.VS.Transcriptome     [功能注释-宿主基因关联分析]
|    ├──01.Procrustes           [普鲁克分析]
|    |  ├──PCA_analysisReport_Omic1.txt       [宿主基因PCA分析报告]
|    |  ├──PCA_analysisReport_Omic2.txt       [扩增子PCA分析报告]
|    |  ├──PCA_Biplot2.png                    [两个组学的PCA双标图]
|    |  ├──Procrustes_analysis_sites.tsv      [普鲁克分析的坐标信息]
|    |  ├──Procrustes_residuals.tsv           [普鲁克分析的残差值信息]
|    |  ├──procrustes_resultPlot.png          [普鲁克分析图]
|    |  ├──Procrustes_resultReport.txt        [普鲁克分析结果报告]
|    |  ├──protest_resultReport.txt           [验证结果报告]
|    |  └──residuals_plot.png                 [残差值图]
|    ├──02.PLS                  [PLS分析]
|    ├──03.RDA_CCA              [RDA/CCA分析]
|    ├──04.RandomForest         [随机森林分析]
|    └──05.SVM                  [支持向量机分析]
└──Species.VS.Transcriptome              [物种注释-宿主基因关联分析]
     └──...

Procrustes分析是一种用于比较两个或多个数据集之间的相似性的方法^[3]，由于扩增子与宿主基因中，存在大量低丰度features，而这些features对于相关性分析贡献度极低，所以进行该模块分析之前，均根据丰度进行了features筛选，Procrustes分析适用于组学关联分析，其主要应用R包vegan完成。这种分析通常涉及到PCA双标图、普氏分析图和残差值图等步骤：

PCA双标图：如图4-1通过主成分分析（PCA），将多维数据降维到较低维度，然后在双标图上展示样本和变量在这些主成分上的分布，以便观察样本之间和变量之间的关系。其中样本和变量在主成分上的投影用箭头和点表示。样本之间的距离和角度反映它们在主成分方向上的相似性或差异性。不同箭头的方向之间的角度可以反映原始特征之间的相关性。如果两个箭头的方向相近，表示对应的特征在数据中可能存在相关性。箭头的长度表示数据在主成分方向上的方差大小。较长的箭头表示在相关主成分上有更大的变化。因此，箭头的长度可以用来衡量特征的重要性，对应的特征在数据变异性中的贡献更大。

为方便用户的图片保存，交互图中单击点或箭头顶端会显示特征的名称信息，双击交互图任意位置可撤回所有显示操作。下载云流程结题报告后，点击右上角相机按钮即可保存实时图片。

功能Procrustes分析结果位置如下：analysis_files/03_Multivariate_Correlation_Analysis/Function.VS.Transcriptome/Procrustes

物种Procrustes分析结果位置如下：analysis_files/03_Multivariate_Correlation_Analysis/Taxa.VS.Transcriptome/Procrustes

图4-1 物种注释-宿主基因 PCA双序图

图4-2 功能注释-宿主基因 PCA双序图

说明：PCA双标图中，点代表样本，箭头代表features；他们之间的夹角代表相关性，夹角越小相关性越大，箭头长度表示features在样本分类中的贡献度。

普鲁克分析图：通过普鲁克分析（Procrustes Analysis）对两个数据集进行旋转变换，使它们在最佳方式下重叠，进一步揭示它们的相似性。结果中得到的旋转矩阵，将一个数据集映射到另一个数据集的坐标系中。旋转图展示了这种映射关系，帮助观察样本或变量之间的相似性。每个线段代表一个样本，线段一端实心圆点代表微生物组数据样本点，线段另一端实心三角形代表相同样本的转录组数据样本点；连线代表两排序构型的矢量残差，可评价二者间的变异情况，连线越短，表示两个数据集之间一致性越高。M平方代表偏差平方和，是数据离散程度的指标。

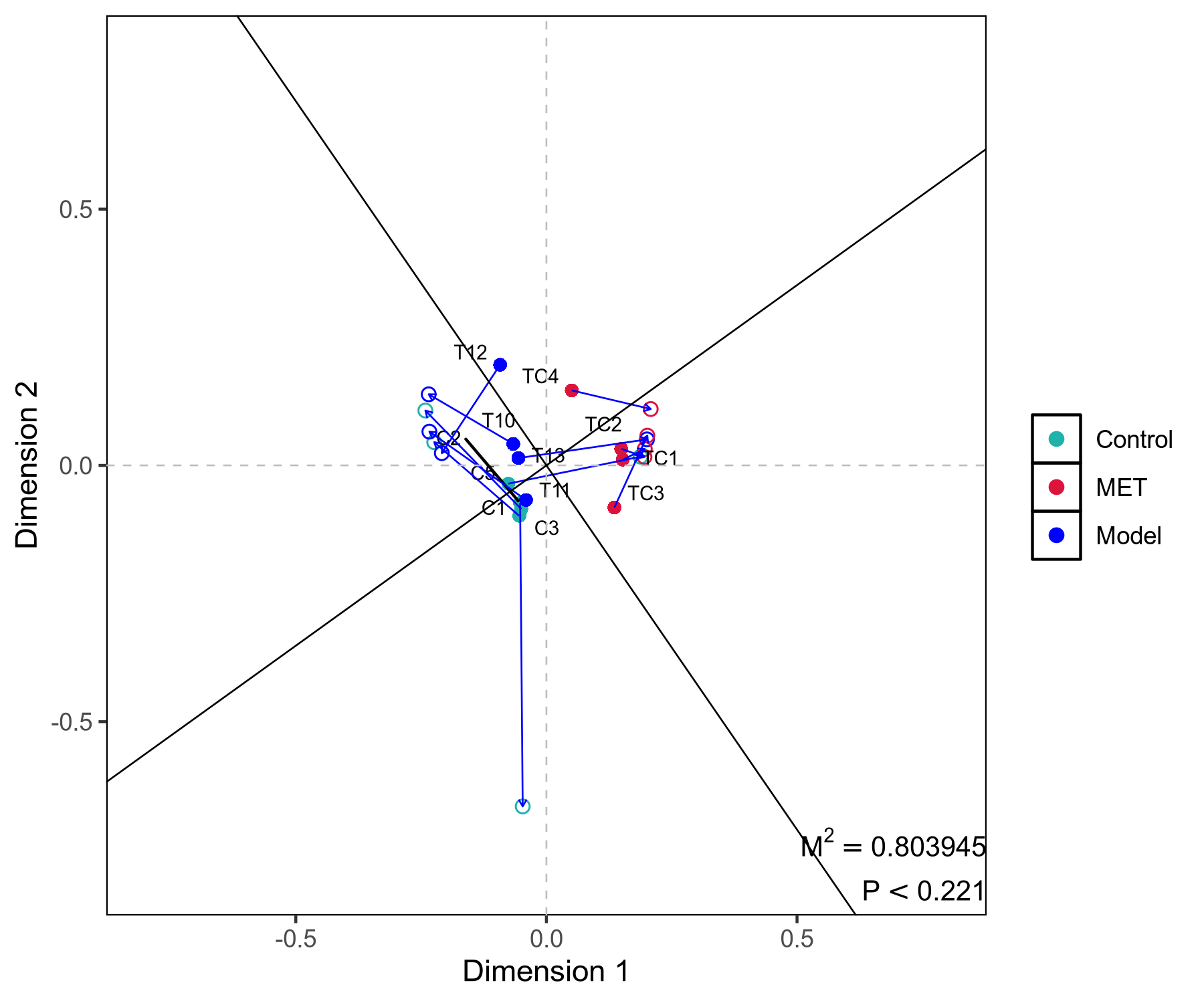
(a)

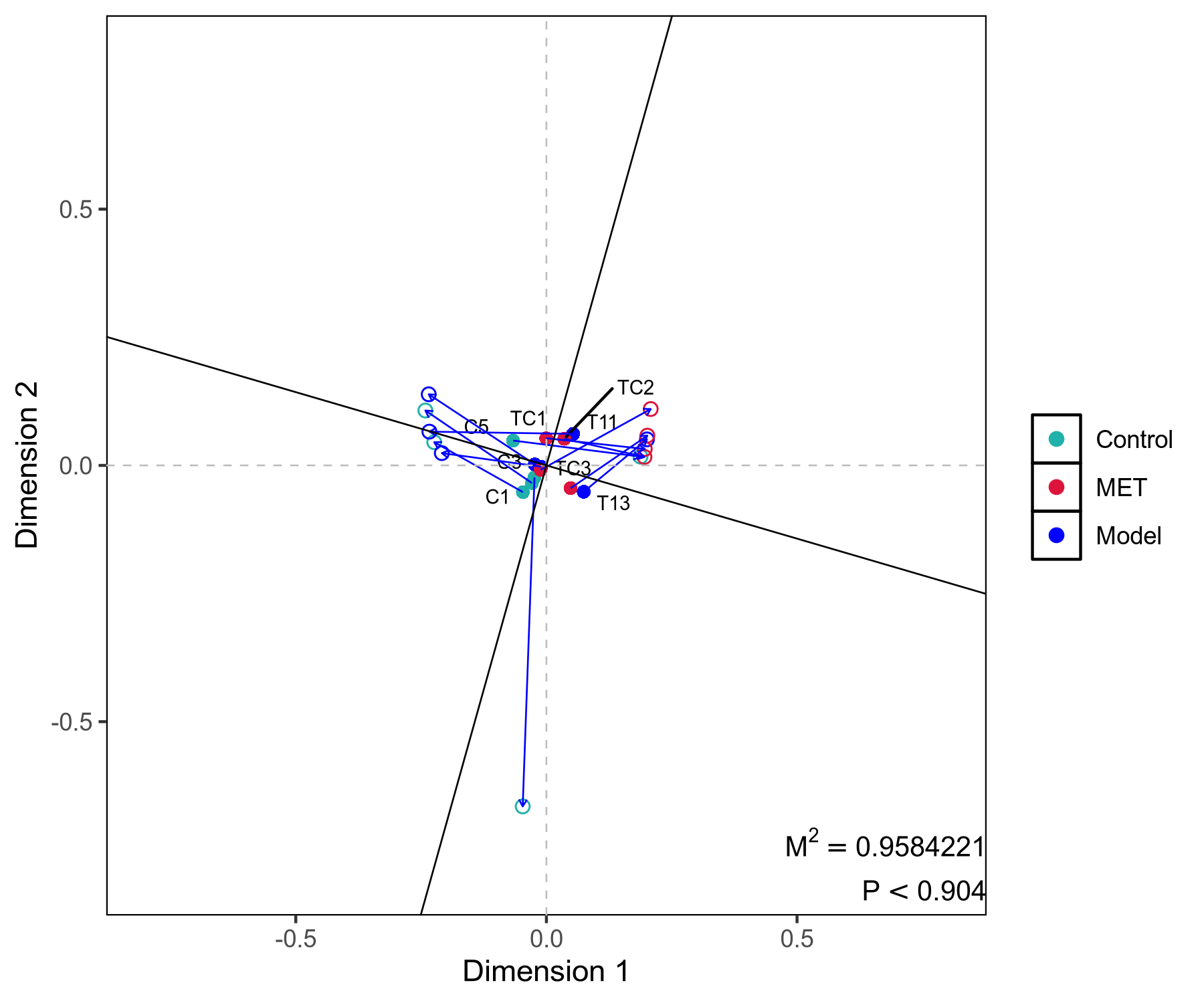
(b)

图5 普鲁克分析图

注：(a)，物种注释-宿主基因普鲁克分析；(b)，功能注释-宿主基因普鲁克分析

说明：每个线段代表一个样本，线段一端实心圆点代表微生物组数据样本点，线段另一端实心三角形代表相同样本的转录组样本点；连线代表两排序构型的矢量残差，可评价二者间的变异情况，连线越短，表示两个数据集之间一致性越高。

残差值图：进行完普鲁克分析之后，通过比较两个数据集在主成分方向上的残差，揭示它们之间的差异。残差是指样本点到主成分方向上的投影点之间的距离，残差值图展示了这些残差，可以帮助识别哪些样本在两个数据集之间差异较大。如果样本中两个组学的组成更为相似，则旋转图中两个匹配的点距离越近，残差较小，反之两个组学无规律，则残差更大。

图6-1 物种注释-宿主基因残差值图

图6-2 功能注释-宿主基因残差值图

说明：残差是指样本点到主成分方向上的投影点之间的距离，残差值图展示了这些残差，两个组学的组成更为相似，残差较小，反之两个组学的分组无规律，则残差更大。

4.2.1.2 PLS分析

03.Multivariate_Correlation_Analysis/
├──Function.VS.Transcriptome     [功能注释-宿主基因关联分析]
|    ├──01.Procrustes           [普鲁克分析]
|    ├──02.PLS                  [PLS分析]
|    |  ├──ModelBuilding_parameters.csv              [PLS建模参数预测结果]
|    |  ├──PLS_Features_correction_BarPlot.png       [载荷值排序图]
|    |  ├──PLS_joint_loadings.png                    [联合载荷图]
|    |  ├──PLS_joint_scores.png                      [联合得分图]
|    |  ├──PLS_loadings.csv                          [联合载荷值信息表]
|    |  └──PLS_scores.csv                            [联合得分值信息表]
|    ├──03.RDA_CCA              [RDA/CCA分析]
|    ├──04.RandomForest         [随机森林分析]
|    └──05.SVM                  [支持向量机分析]
└──Species.VS.Transcriptome      [物种注释-宿主基因关联分析]
     └──...

偏最小二乘法（partial least squares，PLS）PLS分析是一种多变量分析方法，主要用于探索两组变量之间的关系，以揭示变量之间复杂的相互作用和关联。PLS通过寻找最能解释X和Y之间共变异的成分来简化模型，有助于在小样本情况下提高模型的稳定性和预测能力。 PLS分析通过对两个数据组间的整合分析，评估两个数据集之间的内在相关性^[4]。PLS模型一方面可反映不同数据组间的整体影响，另一方面可直接体现不同变量在模型中的权重，权重越大，意味着该变量的变化对另一个组学的扰动更剧烈，应用R包mixOmics进行分析。该分析模块分为三个部分：联合载荷图，联合得分图，关联程度最大的features柱状图。

联合载荷图（Joint loadings plot）：该图显示了两个数据矩阵之间的共同结构，即它们之间的关联性。如果该图是二维散点图，则X轴和Y轴分别代表了PLS第一成分loadings值和PLS第二成分loadings值，每个点表示一个features，点的位置和方向表示该features在两个数据集中的权重和方向。联合载荷图的X轴和Y轴值的大小和方向反映了变量在两个组学数据集之间的关系；正值和负值表示features在两个数据集中的相关性方向，值的大小表示features对另一个组学的关联程度。features在图中的位置和包裹趋势则表明它们在两个数据集中的共同结构上的重要性和方向。这些观察可以帮助解释两个组学数据集之间的关联性和共同模式。

功能PLS分析结果位置如下：analysis_files/03_Multivariate_Correlation_Analysis/Function.VS.Transcriptome/PLS

物种PLS分析结果位置如下：analysis_files/03_Multivariate_Correlation_Analysis/Taxa.VS.Transcriptome/PLS

(a)

(b)

图7 联合载荷图

注：(a)，物种注释-宿主基因联合载荷图；(b)，功能注释-宿主基因联合载荷图

说明：图中的loadings值的大小代表features对模型的贡献程度和组学间的关联程度，正值和负值表示features在两个数据集中的相关性方向。

联合得分图（Joint score plot）：Joint scores图展示了每个样本在PLS中的投影，即它们在共同结构上的表现。这反映了样本在两个数据集之间的关联性。正负值反映了样本在两个组学数据集之间的相关性方向；样本在图中的相对位置反映了它们在两个组学数据集之间的关联性，相邻或聚集的样本可能在两个数据集中表现相似。

(a)

(b)

图8 联合得分图

注：(a)，物种注释-宿主基因联合得分图；(b)，功能注释-宿主基因联合得分图

说明：该图展示了每个样本在PLS中的投影，正负值反映了样本在两个组学数据集之间的相关性方向。

最后选择前两个维度（joint loadings1、joint loadings2）载荷值大小前15的features（关联程度最大）绘制柱状图。特征的loadings值反映了每个特征在投影到潜在变量（latent variables，或称为成分，components）时的权重或贡献。在同一个组学数据中：高loadings值的特征表示这些特征在这一组学数据中与潜在变量之间有强烈的关联。这意味着这些特征在这一组学数据中是非常重要的，它们可能与其他特征之间有较强的相关性。在不同的组学数据之间：高loadings值的特征除了在相同组学数据中存在重要性，除此以外，也意味着这些特征在另一个组学数据的特定生物学过程、途径或状态存在相关性。也就是说loadings越高，与另一组学相关性越强。

(a)

(b)

图9 载荷值排序图

注：(a)，物种注释-宿主基因载荷值排序图；(b)，功能注释-宿主基因载荷值排序图

说明：柱状图中是选取载荷值排名靠前的features进行绘制，载荷值越大，features在两个组学间的关联程度越大。

注意：除了PLS分析探索两个组学相关性以外，云流程中还提供了sPLS(Sparse Partial Least Squares)和O2PLS(Two-way orthogonal partial least squares)分析工具，可在云流程的分步骤部分进行。

4.2.1.3RDA/CCA分析

03.Multivariate_Correlation_Analysis/
├──Function.VS.Transcriptome             [功能注释-宿主基因关联分析]
|    ├──01.Procrustes           [普鲁克分析]
|    ├──02.PLS                  [PLS分析]
|    ├──03.RDA_CCA              [RDA/CCA分析]
|    |  ├──DCA_output.xls                                      [DCA分析结果表格]
|    |  ├──groups_RDA.envfit.xls                               [宿主基因对扩增子影响值表格]
|    |  ├──groups_RDA.Factors.PERMANOVA.xls                    [PERMANOVA分析报告_features因子]
|    |  ├──groups_RDA.features.xls                             [features影响值表格]
|    |  ├──groups_RDA.Group.PERMANOVA.xls                      [PERMANOVA分析报告_样本分组]
|    |  ├──groups_RDA.sample.xls                               [样本影响值表格]
|    |  ├──groups_RDA_features_location_plot.png               [features RDA双序图]
|    |  ├──groups_RDA_sample_location_plot.png                 [样本 RDA双序图]
|    |  └──groups_RDA_sample_location_plot_with_labels.png     [样本 RDA双序图(带标签)]
|    ├──04.RandomForest         [随机森林分析]
|    └──05.SVM                  [支持向量机分析]
└──Species.VS.Transcriptome               [物种注释-宿主基因关联分析]
     └──...

RDA和CCA都属于冗余分析（Redundancy Analysis）的范畴，都是在解释一个变量组对另一个变量组的方差贡献时进行的，云流程会根据数据特点自动挑选RDA或者CCA分析。旨在用统计学手段建立两个组学features之间的回归关系，保留能解释的变异，后将features进行降维，通过夹角指示相关性。箭头的长度表示转录组在RDA轴上的投影的强度，较长的箭头表示该扩增子feature在相应RDA轴方向上的贡献较大，与宿主基因的变化有关，长箭头指示了扩增子feature与宿主基因的关联性更强，对相应的轴有更大的贡献；箭头与宿主基因点的夹角表示宿主基因与扩增子的关联性，以及这个关联性的方向。小夹角表示宿主基因和相应的扩增子特征在RDA轴上有相似的变化趋势，表明它们之间可能存在关联性。样本RDA双序图中的p值反映了分组对微生物差异的解释程度，p小于0.05,则解释方差显著。该部分应用R包vegan进行分析。 RDA1代表的是解释变量对响应变量所解释的最大变异，RDA2 则是次大变异；RDA1和RDA2表示了两个组学features的最大和次大的变化方向。高的 R² 值意味着features对响应变量（另一组学）的关联性有更高的解释能力，也就是关联性更高。

功能RDA/CCA分析结果位置如下：analysis_files/03_Multivariate_Correlation_Analysis/Function.VS.Transcriptome/RDA

物种RDA/CCA分析结果位置如下：analysis_files/03_Multivariate_Correlation_Analysis/Taxa.VS.Transcriptome/RDA

(a)

(b)

图10 features RDA双序图

注：(a)，物种注释-宿主基因 features RDA双序图；(b)，功能注释-宿主基因 features RDA双序图

(a)

(b)

图11 样本RDA双序图

注：(a)，物种注释-宿主基因样本RDA双序图；(b)，功能注释-宿主基因样本RDA双序图

说明：在CCA/RDA排序图内，扩增子组用箭头表示，箭头连线的长度代表某个扩增子feature与转录组分类信息间相关程度的大小（解释方差的大小），箭头越长，说明相关性越大，反之越小。扩增子feature之间的夹角为锐角时表示两个扩增子feature之间呈正相关关系，钝角时呈负相关关系。每个点代表一个宿主基因，点越大，对应丰度越高。宿主基因的点之间，扩增子features与宿主基因之间，扩增子features箭头之间的与原点相连夹角的余弦值近似于相关系数，至于有多近似，就要看RDA1/CCA1和RDA2/CCA2两个坐标轴的解释方差百分比有多大，越大越近似。样本CCA/RDA排序图同理。

4.2.2监督类模型分析

4.2.2.1随机森林

03.Multivariate_Correlation_Analysis/
├──Function.VS.Transcriptome             [功能注释-宿主基因关联分析]
|    ├──01.Procrustes           [普鲁克分析]
|    ├──02.PLS                  [PLS分析]
|    ├──03.RDA_CCA              [RDA/CCA分析]
|    ├──04.RandomForest         [随机森林分析]
|    |  ├──Transcriptome_model_Error_Rate_Curve.png                                   [转录组RandomForest模型错误率曲线图]
|    |  ├──Transcriptome_model_Probability_Graph_Of_Correctly_Classified.png          [转录组RandomForest模型样本裕度图]
|    |  ├──Transcriptome_RFimportance.tsv                                             [转录组RandomForest模型中features重要性信息]
|    |  ├──TranscriptomeROC_curve_specificities_ofRandomForest.tsv                    [转录组RandomForest模型ROC曲线信息]
|    |  ├──Amplicon_model_Error_Rate_Curve.png                                   [扩增子RandomForest模型错误率曲线图]
|    |  ├──Amplicon_model_Probability_Graph_Of_Correctly_Classified.png          [扩增子RandomForest模型样本裕度图]
|    |  ├──Amplicon_RFimportance.tsv                                             [扩增子RandomForest模型中features重要性信息]]
|    |  ├──AmpliconROC_curve_specificities_ofRandomForest.tsv                    [扩增子RandomForest模型ROC曲线信息]
|    |  ├──RFMeanDecreaseAccuracy.png                                               [两个组学RandomForest模型features重要性图]
|    |  └──ROC_of_RFmodel.png                                                       [两个组学RandomForest模型ROC评估曲线图]
|    └──05.SVM                  [支持向量机分析]
└──Species.VS.Transcriptome               [物种注释-宿主基因关联分析]
     └──...

随机森林是一种集成学习方法^[1]，它通过构建多个决策树，每个树都在不同的子样本和特征上训练，最后将它们的结果综合起来。这种集成方法有效地减小了过拟合的风险，并且对于高维数据集表现良好。随机森林能够输出每个特征的重要性评分，即特征对于模型性能的贡献程度。这些重要性分数可以用来筛选最相关的特征，帮助识别与实验组和对照组差异相关的生物学特征。随机森林关联分析的目的是利用多个决策树的集成效果，获取两种组学间，各features的重要性比较，并通过不同组学的单独建模的ROC曲线（受试者回归曲线， Receiver Operating Characteristic curve）对比，评估哪种组学能更好地分离对照组和实验组。该部分应用R包randomForest进行分析。

注意：在多分类模型中（分组方案中存在多个分组），绘制ROC曲线通常是通过将每个类别与其他所有类别结合起来进行二分类来完成的。这是因为ROC曲线是针对二分类问题设计的，它显示了真正例率（True Positive Rate，也称为灵敏度）和假正例率（False Positive Rate）之间的关系。在多分类情况下，可以将每个类别视为一个正例，其他所有类别合并为一个负例，然后分别计算每个类别的真正例率和假正例率，最终将这些结果绘制在同一张ROC曲线上。

图12-1 物种注释-宿主基因随机森林features重要性排序图

图12-2 功能注释-宿主基因随机森林features重要性排序图

说明：重要性图中的横坐标是Mean Decrease Accuracy，它衡量了每个features在随机森林中的重要性。重要性越大，features对样本分组的贡献性越大。

图13-1 物种注释-宿主基因随机森林模型ROC图

图13-2 功能注释-宿主基因随机森林模型ROC图

说明：ROC图中的横坐标为准确度，纵坐标为敏感度，准确度和敏感度越高，模型的预测效果越好。 AUC为曲线下面积，曲线下面积越接近1，模型预测效果越好。可根据AUC曲线情况评估哪种组学能更好地分离对照组和实验组。

4.2.2.2支持向量机

03.Multivariate_Correlation_Analysis/
├──Function.VS.Transcriptome             [功能注释-宿主基因关联分析]
|    ├──01.Procrustes           [普鲁克分析]
|    ├──02.PLS                  [PLS分析]
|    ├──03.RDA_CCA              [RDA/CCA分析]
|    ├──04.RandomForest         [随机森林分析]
|    └──05.SVM                  [支持向量机分析]
|       ├──Transcriptome_SVM_features_importance.tsv              [转录组SVM模型features重要性信息]
|       ├──TranscriptomeROC_curve_specificities_ofSVM.tsv         [转录组SVM模型ROC曲线信息]
|       ├──Amplicon_SVM_features_importance.tsv                   [扩增子SVM模型features重要性信息]
|       ├──AmpliconROC_curve_specificities_ofSVM.tsv              [扩增子SVM模型ROC曲线信息]
|       ├──ROC_of_SVMmodel.png                                    [两个组学SVM模型ROC曲线图]
|       └──SVM_FeaturesImportance.png                             [两个组学SVM模型features重要性图]
└──Species.VS.Transcriptome               [物种注释-宿主基因关联分析]
        └──...

支持向量机是一种监督学习算法^[5]，其目标是找到一个超平面，将不同类别的样本分隔开。在生物信息学中，SVM可以用于分类和回归任务。SVM在分类问题中对样本之间的复杂关系有较好的拟合能力。支持向量机的支持向量也可以提供有关差异性特征的信息。除了两个组学features比较以外，与随机森林一样，提供组学分别建模的ROC曲线比较。

扩增子和宿主基因的数据通常是高维度的，其中包含了大量的features。随机森林在高维数据中表现优异，因为它可以自动选择子集进行训练，从而减小过拟合风险。相比之下，支持向量机在高维数据中的性能高度依赖于核函数的选择和参数调整；随机森林相对于异常值具有较好的鲁棒性，因为它基于多个决策树的综合结果，异常值对于整体的影响较小。支持向量机在某些情况下可能对异常值较为敏感，因为它试图找到一个全局最优的超平面，受到极端值的影响较大。该部分应用R包e1071进行分析。

图14-1 物种注释-宿主基因支持向量机features重要性排序图

图14-2 功能注释-宿主基因支持向量机features重要性排序图

说明：重要性图中的横坐标是支持向量机的平均重要性，重要性越大，feature对样本分组的贡献性越大。

图15-1 物种注释-宿主基因支持向量机模型ROC图

图15-2 功能注释-宿主基因支持向量机模型ROC图

五、分析所用软件的版本

软件	版本
ggplot2	4.2.3
vegan	4.2.3
OmicsPLS	4.2.3
igraph	4.2.3
pheatmap	4.2.3
randomForest	4.2.2
e1071	4.2.3
pROC	4.2.3
mixOmics	6.20.0
pheatmap	1.0.12

六、参考文献

[1] Breiman L. Random Forests. Machine Learning, 2001 45(1), 5-32.

[2] Ito K., Murphy D. Application of ggplot2 to Pharmacometric Graphics. CPT Pharmacomet. Syst. Pharmacol, 2013 2, 79.

[3] Rohlf J. Shape Statistics: Procrustes Superimpositions and Tangent Spaces. Journal of Classification, 1999 16(2), 197-223.

[4] Trygg J., Wold, S. Orthogonal Projections to Latent Structures (O-PLS). Journal of Chemometrics: A Journal of the Chemometrics Society, 2003 17(3), 119-128.

[5] Cortes C., Vapnik V. Support-Vector Networks. Machine Learning, 1995 20(3), 273-297.

[6] Love I., Huber W., Anders S. Moderated Estimation of Fold Change and Dispersion for RNA-seq Data with Deseq2. Genome Biology, 2014 15(12), 550.

[7] Smyth K. edgeR: a Bioconductor Package for Differential Expression Analysis of Digital Gene Expression Data. Bioinformatics, 2010. 26(1), 139.